Nephroid
A mesmerizing curve that never fails to fascinate mathematicians and enthusiasts alike, the nephroid is a stunning curve that instantly catches the eye. Its unique shape and properties make it a topic of interest for many.
Pain Points of Nephroid
While not a harmful curve in any way, some may find it challenging to understand the mathematical jargon surrounding it. The unfamiliar terms may be a barrier to newcomers wanting to explore the subject. However, with a bit of digging, the curve's marvels can be unearthed.
Target of Nephroid
The nephroid has intrigued mathematicians for centuries with its unique properties, and it continues to be an area of research. It is a subjective and objective target that interests anyone with a passion for mathematics, physics, and engineering. Additionally, the elegance of the nephroid makes it a visually appealing subject that artists may incorporate in their work.
Summary of Main Points on Nephroid
The nephroid is a fascinating geometric curve that has captured the attention of many. With a unique shape, it attracts enthusiasts, artists, mathematicians, physicists, and engineers alike. While the terminology surrounding the subject may seem intimidating, the curve's elegance and properties make it worth exploring.
Nephroid Analysis
The nephroid is a curve with two cusps formed by the path traced out by a point on a circle as it rolls without slipping around a fixed circle of the same radius. It comes from the Greek word for "kidney," which describes its form.
When it's rolled, the path appears to generate a three-leaf clover shape, with the center of each cusp lying on the circumference of the other circle. The nephroid exhibits fascinating properties such as constant curvature, meaning it can be used to make accurate gear teeth. Its stunning symmetry is pleasing to the eye, which makes it noteworthy for artists. Mathematical research shows that it has interesting properties that don't require advanced mathematical knowledge to explore.
Applications of Nephroid
The nephroid has practical uses as well. As mentioned, it can make accurate gear teeth, which has been put to use in practical applications such as timepieces and industrial machinery. Furthermore, the curve has applications in kinematics, where it is used to analyze the motion of two colliding objects.
Other Properties of Nephroid
The nephroid has been a topic of mathematical research due to its fascinating properties. One such property is its relationship to the bicorn curve. When the nephroid is dilated, the bicorn curve is formed, and vice versa. Additionally, the nephroid is a roulette, meaning that it results from the path a point on a circle traces as it rolls around another circle.
Frequently Asked Questions about Nephroid
Here are some commonly asked questions about the nephroid:
What is the significance of the nephroid?
The nephroid has properties that make it fascinating to mathematicians and enthusiasts alike. It has practical applications in the making of gear teeth, and it has interesting symmetrical properties. Additionally, it has sparked interest in artists and has been featured in art forms such as tattoos.
Who discovered the nephroid?
The nephroid has been known since ancient times, but Galileo Galilei and Giovanni Domenico Cassini were the first to study its properties in-depth.
What is the equation of the nephroid?
The nephroid's parametric equations can be written as follows:
x=a(t-sint), y=a(1-cost)
What other curves are related to the nephroid?
The bicorn curve is related to the nephroid, and when the nephroid is dilated, the bicorn curve is formed.
Conclusion of Nephroid
The nephroid is a fascinating curve that has intrigued mathematicians, physicists, engineers, and artists alike. Its unique symmetrical properties make it visually appealing, and its practical uses in gear-making and kinematics add to its significance. While its terminology and properties can seem intimidating, exploring the nephroid can be a rewarding experience for anyone with a passion for mathematics or the arts.
Gallery
Nephroid
Photo Credit by: bing.com / radial pedal rose dir
Don Cole
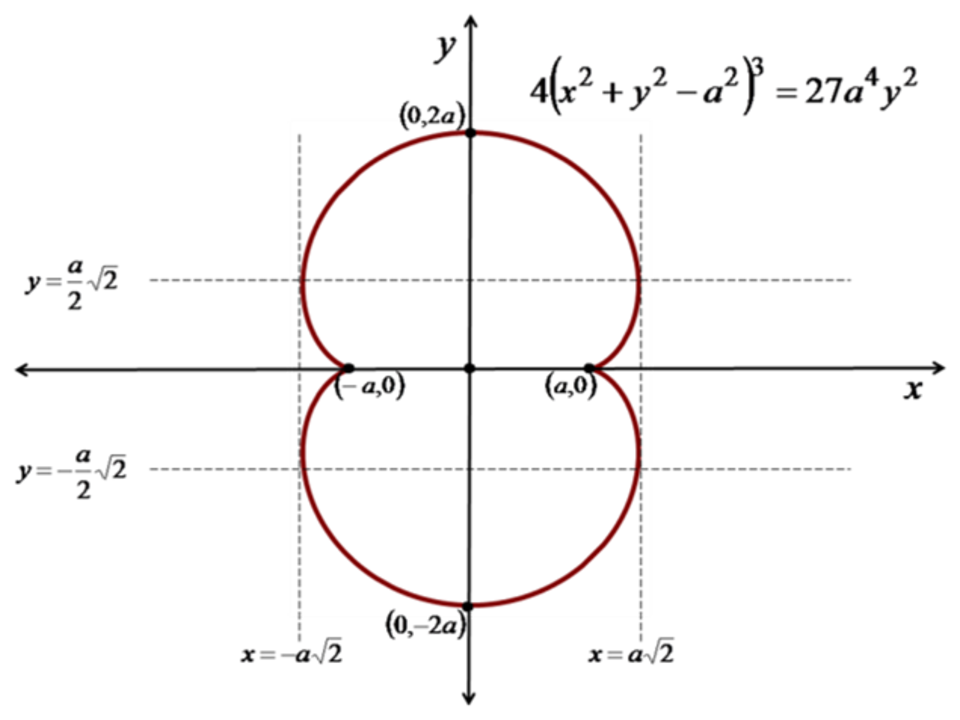
Photo Credit by: bing.com /
Nephroid -- From Wolfram MathWorld
Photo Credit by: bing.com / wolfram mathworld cusped
Nephroid
Photo Credit by: bing.com / history equation cartesian parametric ac
Nephroid
Photo Credit by: bing.com / dir